2020. 3. 4. 03:43ㆍ카테고리 없음
The spline space Cr k (∆) attached to a subdivided domain ∆ of Rd is the vector space of functions of class Cr which are polynomials of degree ≤ k on each piece of this subdivision. Classical splines on planar rectangular grids play an important role in Computer Aided Geometric Design, and spline spaces over arbitrary subdivisions of planar domains are now considered for isogeometric analysis applications. We address the problem of determining the dimension of the space of bivariate splines Cr k (∆) for a triangulated region ∆ in the plane. Using the homological introduced by Billera (1988), we number the vertices and establish a formula for an upper bound on the dimension. There is no restriction on the ordering and we obtain more accurate approximations to the dimension than previous methods and furthermore, in certaincasesevenanexactvaluecanbe found. Theconstruction makes also possible to get a short proof for the dimension formula when k ≥ 4r+1, and the same method we use in this proof yields the dimension straightaway for many other cases.
We consider the functional linear regression model where the ex-planatory variable is a random surface and the response is a real ran-dom variable, with bounded or normal noise. Bivariate splines over triangulations represent the random surfaces. We use this represen-tation to construct least squares estimators of the regression function with or without a penalization term.
Under the assumptions that the regressors in the sample are bounded and span a large enough space of functions, bivariate splines approximation properties yield the con-sistency of the estimators. Simulations demonstrate the quality of the asymptotic properties on a realistic domain. We also carry out an application to ozone concentration forecasting over the US that illustrates the predictive skills of the method. We present two numerical methods for the fully nonlinear elliptic Monge-Ampère equation.
The first is a pseudo transient continuation method and the second is a pure pseudo time marching method. The methods are proved to con-verge to a convex solution of a natural discrete variational formulation with C1 conforming approximations.
The assumption of existence of a convex solution to the discrete problem is proven for smooth solutions of the continuous problem and supported by numerical evidence for non smooth solutions. A uniform inf–sup condition related to a parameter dependent Stokes problem is established. Such conditions are intimately connected to the construction of uniform preconditioners for the problem, i.e., preconditioners which behave uniformly well with respect to variations in the model parameter as well as the discretization parameter. For the present model, similar results have been derived before, but only by utilizing extra regularity ensured by convexity of the domain. The purpose of this paper is to remove this artificial assumption. As a byproduct of our analysis, in the two dimensional case we also construct a new projection operator for the Taylor–Hood element which is uniformly bounded in L2 and commutes with the divergence operator.
This construction is based on a tight connection between a subspace of the Taylor–Hood velocity space and the lowest order Nedelec edge element. Smooth trivariate splines on uniform tetrahedral partitions are well suited for high-quality visualization of isosurfaces from scalar volumetric data. We propose a novel rendering approach based on spline patches with low total degree, for which ray-isosurface intersections are computed using efficient root finding algorithms.
Smoothly varying surface normals are directly extracted from the underlying spline representation. Our approach is using a combined CUDA and graphics pipeline and yields two key advantages over previous work. First, we can interactively vary the isovalues since all required processing steps are performed on the GPU. Second, we employ instancing in order to reduce shader complexity and to minimize overall memory usage. In particular, this allows to compute the spline coefficients on-the-fly in real-time on the GPU. A number of useful bivariate spline methods are global in nature, i.e., all of the coefficients of an approximating spline must be computed at one time.
Typically this involves solving a system of linear equations. Examples include several well-known methods for fitting scattered data, such as the minimal energy, least-squares, and penalized least-squares methods. Finite-element methods for solving boundary-value problems are also of this type. It is shown here that these types of globally-defined splines can be efficiently computed, provided we work with spline spaces with stable local minimal determining sets. Bivariate splines defined over triangulations are important tools in several application areas including scattered data fitting and the numerical solution of boundaryvalue problems by the finite element method. Methods for computing spline approximations fall into two classes.
We prove that a planar C2-regular boundary Γ can always be parameterized with its closest point projection pi over a certain collection of edges Γh in an ambient triangulation, by making simple assumptions on the background mesh. For Γh, we select the edges that have both vertices on one side of Γ and belong to a triangle that has a vertex on the other side. By assuming a quasi-uniform family of background meshes, a sufficiently small mesh size h and that certain angles in each mesh are acute, we prove that pi: Γh → Γ is a homeomorphism and that it is C1 on each edge in Γh. We provide bounds for the Jacobian of the parameterization and local estimates for the required mesh size, which could be used in adapting the ambient triangulation. Such a parameterization was first proposed in 17 where it was applied to the construction of a high-order immersed boundary method on a class of planar piecewise C2-curves. Curve parameterization; closest point projection; immersed boundary AMS subject classifications.


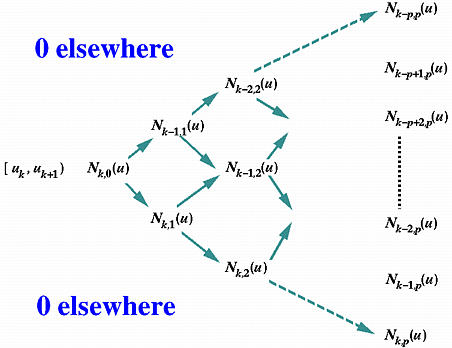
Linear Spline Function
68U05, 65D18 1.